1. Linear and Logistic Regression

This tutorial shows how to apply linear regression and logistic regression using PyTorch.

import numpy as np
import pandas as pd

# visualization libraries
from matplotlib import pyplot as plt
import plotly.express as px
import plotly.graph_objects as go

# pytorch dependencies
import torch
import torch.nn as nn
from torch.utils.data import DataLoader, TensorDataset

1.1. Linear Regression

1.1.1. Problem setting

• Given: A set of measurement pairs \(\left\{x^{(i)}, y^{\text {(i)}}\right\}_{i=1,...m}\) with \(x \in \mathbb{R}^{n}\) and \(y \in \mathbb{R}\)

• Question: If I give you a novel \(x\), what would be your best guess about its corresponding \(y\)?

• Linear regression assumption:

\[y \approx h(x)=\vartheta^{\top} x = \vartheta_0 + \vartheta_1 \cdot x_1 + ... \vartheta_n \cdot x_n\]

Note: \(\vartheta_0\) is the so called bias term and you can read more about it in the “Analytical Solution” subsection below.

In matrix form this becomes:

\[Y \approx X \vartheta\]

As a reminder, we can interpret the linear dependence assumption as a Maximum Likelihood Estimation of the “true” underlying linear dependence between inputs \(x\) and outputs \(y\) with added Gaussian noise on top:

\[Y = X \vartheta + \epsilon, \quad \text{with} \; \epsilon \sim \mathcal{N}(0,\sigma^2), \; \epsilon \in \mathbb{R}^n\]

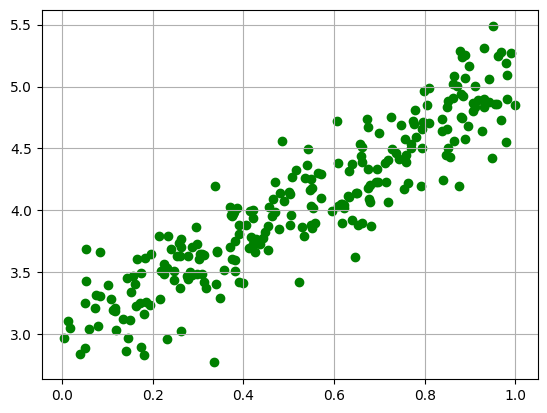
1.1.2. Artificial Dataset

a = 3
b = 2
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = a + b*x + noise

For convenience, we use Pandas to store our values in the dataframe and then access them out of the dataframe - this is a highly common workflow for machine learning datasets. A normal split would be a Pandas dataframe for labels, serial data etc. and images in the same folder, which can then be described with the PyTorch DataSet API.

df = pd.DataFrame()
df['x'] = x
df['y'] = y

plt.scatter(df['x'], df['y'], color='green')
plt.grid()
plt.show()

1.1.3. Gradient Descent Optimization

In the lecture we saw that for an iterative optimization process, e.g. gradient descent, we need to define a measure \(J\), which capture the error. This quantity is what we essentially minimize through repeated updates of the parameters \(\vartheta\). One very common error function \(J\), a.k.a. loss or as PyTorch calls it criterion, is the mean squared error (MSE), a.k.a. squared L2 loss:

\[J(\vartheta)=\frac{1}{2} \sum_{i=1}^{m}\left(h\left(x^{(i)}\right)-y^{(i)}\right)^{2}\]

# Reshape the input variables
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

# Definition of the linear regression model


class LinearRegressionModel(nn.Module):

    def __init__(self, input_dim, output_dim):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(input_dim, output_dim)

    def forward(self, x):
        out = self.linear(x)
        return out


input_dim = x_train.shape[1]
output_dim = y_train.shape[1]

learning_rate = 0.01
epochs = 100

model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

print("Test the performance of the model ** before ** we do any optimization: ")

with torch.no_grad():
    predicted = model(torch.from_numpy(x_train)).data.numpy()

plt.clf()
plt.plot(x_train, y_train, 'go', label='True data')
plt.plot(x_train, predicted, '.', label='Predictions')
plt.legend()
plt.grid()
plt.show()

Test the performance of the model ** before ** we do any optimization: 

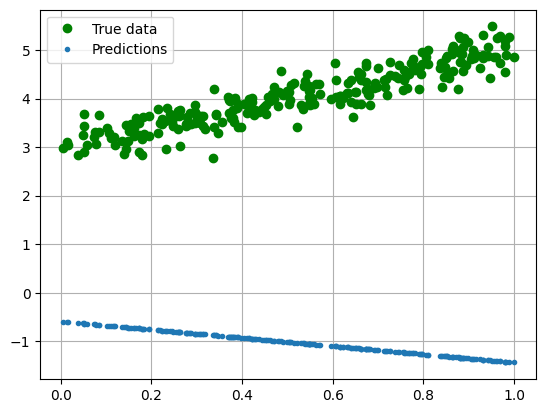
The model is currently initialized with some random numbers. These are:

for name, param in model.named_parameters():
  print(name, ": ", param.data)
  # bias = \vartheta_0
  # weight = \vartheta_1:n

linear.weight :  tensor([[-0.8471]])
linear.bias :  tensor([-0.5895])

for epoch in range(epochs):

    inputs = torch.from_numpy(x_train)
    y_train_var = torch.from_numpy(y_train)

    # Clear gradient buffer
    optimizer.zero_grad()

    # Output from model given the inputs
    y_pred = model(inputs)

    # Get loss for the model's prediction
    loss = criterion(y_pred, y_train_var)
    loss.backward()

    # Update the model's parameters
    optimizer.step()

    print('epoch {}, loss {}'.format(epoch, loss.item()))

epoch 0, loss 26.55284309387207
epoch 1, loss 25.201623916625977
epoch 2, loss 23.919395446777344
epoch 3, loss 22.70265007019043
epoch 4, loss 21.548030853271484
epoch 5, loss 20.452369689941406
epoch 6, loss 19.41265869140625
epoch 7, loss 18.42603302001953
epoch 8, loss 17.489789962768555
epoch 9, loss 16.601354598999023
epoch 10, loss 15.758282661437988
epoch 11, loss 14.958258628845215
epoch 12, loss 14.19908618927002
epoch 13, loss 13.478677749633789
epoch 14, loss 12.795053482055664
epoch 15, loss 12.14633560180664
epoch 16, loss 11.530740737915039
epoch 17, loss 10.946579933166504
epoch 18, loss 10.392244338989258
epoch 19, loss 9.866212844848633
epoch 20, loss 9.367040634155273
epoch 21, loss 8.893355369567871
epoch 22, loss 8.443855285644531
epoch 23, loss 8.017306327819824
epoch 24, loss 7.612534999847412
epoch 25, loss 7.22843074798584
epoch 26, loss 6.8639373779296875
epoch 27, loss 6.51805305480957
epoch 28, loss 6.1898274421691895
epoch 29, loss 5.878359794616699
epoch 30, loss 5.582794666290283
epoch 31, loss 5.302318572998047
epoch 32, loss 5.036160945892334
epoch 33, loss 4.7835917472839355
epoch 34, loss 4.54391622543335
epoch 35, loss 4.316476821899414
epoch 36, loss 4.100647449493408
epoch 37, loss 3.895836353302002
epoch 38, loss 3.7014806270599365
epoch 39, loss 3.5170464515686035
epoch 40, loss 3.342026710510254
epoch 41, loss 3.175940752029419
epoch 42, loss 3.0183327198028564
epoch 43, loss 2.8687691688537598
epoch 44, loss 2.726839780807495
epoch 45, loss 2.592154026031494
epoch 46, loss 2.4643428325653076
epoch 47, loss 2.343055248260498
epoch 48, loss 2.2279574871063232
epoch 49, loss 2.1187338829040527
epoch 50, loss 2.0150840282440186
epoch 51, loss 1.9167237281799316
epoch 52, loss 1.8233823776245117
epoch 53, loss 1.7348039150238037
epoch 54, loss 1.6507456302642822
epoch 55, loss 1.5709757804870605
epoch 56, loss 1.4952760934829712
epoch 57, loss 1.4234389066696167
epoch 58, loss 1.3552664518356323
epoch 59, loss 1.2905715703964233
epoch 60, loss 1.2291768789291382
epoch 61, loss 1.1709140539169312
epoch 62, loss 1.1156229972839355
epoch 63, loss 1.0631520748138428
epoch 64, loss 1.013357162475586
epoch 65, loss 0.9661014676094055
epoch 66, loss 0.921255350112915
epoch 67, loss 0.8786958456039429
epoch 68, loss 0.8383062481880188
epoch 69, loss 0.7999756932258606
epoch 70, loss 0.7635990381240845
epoch 71, loss 0.7290766835212708
epoch 72, loss 0.6963138580322266
epoch 73, loss 0.6652204990386963
epoch 74, loss 0.635711669921875
epoch 75, loss 0.6077063679695129
epoch 76, loss 0.5811278223991394
epoch 77, loss 0.5559030175209045
epoch 78, loss 0.5319631099700928
epoch 79, loss 0.5092422962188721
epoch 80, loss 0.48767825961112976
epoch 81, loss 0.46721208095550537
epoch 82, loss 0.44778764247894287
epoch 83, loss 0.4293518662452698
epoch 84, loss 0.4118541181087494
epoch 85, loss 0.39524656534194946
epoch 86, loss 0.37948372960090637
epoch 87, loss 0.3645226061344147
epoch 88, loss 0.3503219187259674
epoch 89, loss 0.33684325218200684
epoch 90, loss 0.32404956221580505
epoch 91, loss 0.3119059205055237
epoch 92, loss 0.3003791272640228
epoch 93, loss 0.2894377112388611
epoch 94, loss 0.27905166149139404
epoch 95, loss 0.2691928446292877
epoch 96, loss 0.2598342299461365
epoch 97, loss 0.25095024704933167
epoch 98, loss 0.2425166666507721
epoch 99, loss 0.23451057076454163

with torch.no_grad():
    predicted = model(torch.from_numpy(x_train)).data.numpy()

plt.clf()
plt.plot(x_train, y_train, 'go', label='True data')
plt.plot(x_train, predicted, '.', label='Predictions')
plt.legend()
plt.grid()
plt.show()

for name, param in model.named_parameters():
  print(name, ": ", param.data)

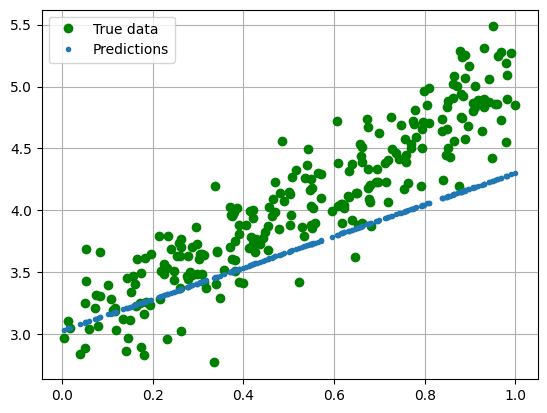
linear.weight :  tensor([[1.2722]])
linear.bias :  tensor([3.0305])

1.1.4. Stochastic Gradient Descent

We can run the same optimization, but on chunks of the data, a.k.a. minibatches. This variant of gradient descent is then called Stochastic Gradient Descent due to the stochastic nature of optimizing \(\vartheta\) on subsets of the data.

batch_size = 32
num_batches = len(x) // batch_size
batch_idxs = np.arange(num_batches)

for epoch in range(epochs):
    np.random.shuffle(batch_idxs)

    for i in batch_idxs:
        # slice out the portion of x and y, which corresponds to the batch i
        x_batch = x_train[batch_size*i:batch_size*(i+1)]
        y_batch = y_train[batch_size*i:batch_size*(i+1)]

        inputs = torch.from_numpy(x_batch)
        y_train_var = torch.from_numpy(y_batch)

        # Clear gradient buffer
        optimizer.zero_grad()

        # Output from model given the inputs
        y_pred = model(inputs)

        # Get loss for the model's prediction
        loss = criterion(y_pred, y_train_var)
        loss.backward()

        # Update the model's parameters
        optimizer.step()

    print('epoch {}, loss {}'.format(epoch, loss.item()))

epoch 0, loss 0.15132689476013184
epoch 1, loss 0.15757179260253906
epoch 2, loss 0.12175792455673218
epoch 3, loss 0.09626052528619766
epoch 4, loss 0.09974482655525208
epoch 5, loss 0.096749447286129
epoch 6, loss 0.0932689905166626

epoch 7, loss 0.10538350045681
epoch 8, loss 0.08690407872200012
epoch 9, loss 0.09966102987527847
epoch 10, loss 0.08320625126361847
epoch 11, loss 0.08237418532371521
epoch 12, loss 0.10202844440937042
epoch 13, loss 0.10169750452041626
epoch 14, loss 0.10134657472372055
epoch 15, loss 0.06312520802021027
epoch 16, loss 0.054866619408130646
epoch 17, loss 0.09381613880395889
epoch 18, loss 0.05409059673547745
epoch 19, loss 0.09274499118328094
epoch 20, loss 0.09222377091646194
epoch 21, loss 0.0768422931432724
epoch 22, loss 0.07648130506277084
epoch 23, loss 0.05282335728406906
epoch 24, loss 0.07568173855543137
epoch 25, loss 0.0841827243566513
epoch 26, loss 0.08922847360372543
epoch 27, loss 0.07485192269086838
epoch 28, loss 0.09587374329566956
epoch 29, loss 0.08275765180587769
epoch 30, loss 0.05768406391143799
epoch 31, loss 0.07379080355167389
epoch 32, loss 0.05148899182677269
epoch 33, loss 0.08604416996240616
epoch 34, loss 0.0728679969906807
epoch 35, loss 0.051112979650497437
epoch 36, loss 0.08479645103216171
epoch 37, loss 0.07233914732933044
epoch 38, loss 0.07987968623638153
epoch 39, loss 0.056118834763765335
epoch 40, loss 0.0715007558465004
epoch 41, loss 0.05050215870141983
epoch 42, loss 0.055717140436172485
epoch 43, loss 0.09043440967798233
epoch 44, loss 0.07816328853368759
epoch 45, loss 0.07027234137058258
epoch 46, loss 0.07037530094385147
epoch 47, loss 0.06972038000822067
epoch 48, loss 0.0770694836974144
epoch 49, loss 0.08001921325922012
epoch 50, loss 0.05482156202197075
epoch 51, loss 0.049791522324085236
epoch 52, loss 0.08772119879722595
epoch 53, loss 0.08743599057197571
epoch 54, loss 0.06886529922485352
epoch 55, loss 0.06867704540491104
epoch 56, loss 0.06820297986268997
epoch 57, loss 0.06803512573242188
epoch 58, loss 0.08613117784261703
epoch 59, loss 0.06770454347133636
epoch 60, loss 0.07428763061761856
epoch 61, loss 0.08538898080587387
epoch 62, loss 0.06752943247556686
epoch 63, loss 0.06710097193717957
epoch 64, loss 0.07347144186496735
epoch 65, loss 0.07538165897130966
epoch 66, loss 0.07309751212596893
epoch 67, loss 0.04916081950068474
epoch 68, loss 0.0666542649269104
epoch 69, loss 0.04912230744957924
epoch 70, loss 0.07234420627355576
epoch 71, loss 0.07392998039722443
epoch 72, loss 0.06491353362798691
epoch 73, loss 0.08275939524173737
epoch 74, loss 0.06584985554218292
epoch 75, loss 0.08240757137537003
epoch 76, loss 0.06432017683982849
epoch 77, loss 0.06548000127077103
epoch 78, loss 0.0652213916182518
epoch 79, loss 0.07084168493747711
epoch 80, loss 0.06511659175157547
epoch 81, loss 0.08132227510213852
epoch 82, loss 0.05235873907804489
epoch 83, loss 0.06338775157928467
epoch 84, loss 0.07012397795915604
epoch 85, loss 0.06313913315534592
epoch 86, loss 0.06984704732894897
epoch 87, loss 0.06433412432670593
epoch 88, loss 0.06424663215875626
epoch 89, loss 0.06948049366474152
epoch 90, loss 0.069351926445961
epoch 91, loss 0.048958670347929
epoch 92, loss 0.06389067322015762
epoch 93, loss 0.06965489685535431
epoch 94, loss 0.06375724077224731
epoch 95, loss 0.05171549692749977
epoch 96, loss 0.06861113011837006
epoch 97, loss 0.048993583768606186
epoch 98, loss 0.05160181224346161
epoch 99, loss 0.06826980412006378

Test the performance of the model after optimization:

with torch.no_grad():
    predicted = model(torch.from_numpy(x_train)).data.numpy()

plt.clf()
plt.plot(x_train, y_train, 'go', label='True data')
plt.plot(x_train, predicted, '.', label='Predictions')
plt.legend()
plt.grid()
plt.show()

for name, param in model.named_parameters():
  print(name, ": ", param.data)

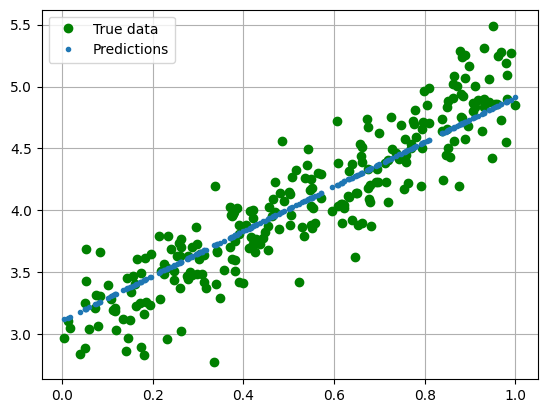
linear.weight :  tensor([[1.8016]])
linear.bias :  tensor([3.1119])

1.1.5. Analytical Solution

As we saw in the lecture, the linear regression problem is one of the very few machine learning algorithms which admits an analytical solution. This reads

\[ \quad\vartheta=\left(X^{\top}X\right)^{-1}X^{\top}Y \]

Caution: To get the so called bias term \(\vartheta_0\), we need to extend \(X\) to

\[\begin{split}X_{m \times n}=\left[\begin{array}{c}x^{(1) \top }\\ \vdots \\ x^{(m) \top}\end{array} \mathbf{1} \right],\end{split}\]

otherwise we assume that the line we are fitting crosses \(y\) at \(x=0\). The PyTorch model we saw before automatically defines a bias term and optimizes it to the data.

# extended x vector
x_ext = np.ones((x.shape[0], 2))
x_ext[:,0] = x

xtx = x_ext.T.dot(x_ext)
xtx_inv = np.linalg.inv(xtx)
xtx_inv_xt = xtx_inv.dot(x_ext.T)
theta = xtx_inv_xt.dot(y)

print("theta =", theta)

theta = [2.04017376 2.97868312]

1.1.6. Exercise

Apply linear regression on the housing price dataset provided here using:

1. Gradien Descent

2. Stochastic Gradient Descent

3. Analytical Solution

Note: there won’t be a solution to this exercise. It is only provided as practice material.

Hint: You might find this helpful.

####################
# TODO


####################

1.2. Logistic Regression

1.2.1. Problem setting

• Given: given is a set of measurement pairs \(\left\{x^{(i)}, y^{\text {(i)}}\right\}_{i=1,...m}\) with \(x \in \mathbb{R}^{n}\) and \(y \in \{0,1\}\)

• Question: if a give you a novel \(x\), what would be your best guess about its corresponding \(y\)? Up until here, the only difference to linear regression is in the domain of \(y\).

• Logistic regression assumption: Instead of asking directly whether the class is 0 or 1, we model the probability of the class being 1 with \(h\): $\(h(x) = \varphi \left( \vartheta^{\top} x \right) = \frac{1}{1+e^{-\vartheta^{\top} x}} = \frac{1}{1+e^{-(\vartheta_0 + \vartheta_1 \cdot x_1 ... + \vartheta_n \cdot x_n)}} \)$

Sigmoid function:

Note: Unfortunately, even this very simple classification model does not have an analytical solution, thus we use gradient-based optimization.

Reference: this implementation is a simplification of the example given here.

1.2.2. Iris Dataset

# get iris dataset
from urllib.request import urlretrieve
iris = 'http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
urlretrieve(iris)
df0 = pd.read_csv(iris, sep=',')

# name columns
attributes = ["sepal_length", "sepal_width",
              "petal_length", "petal_width", "class"]
df0.columns = attributes

# add species index
species = list(df0["class"].unique())
df0["class_idx"] = df0["class"].apply(species.index)

print(df0.head())
print("Count occurence of each class:")
print(df0["class"].value_counts())

   sepal_length  sepal_width  petal_length  petal_width        class  \
0           4.9          3.0           1.4          0.2  Iris-setosa   
1           4.7          3.2           1.3          0.2  Iris-setosa   
2           4.6          3.1           1.5          0.2  Iris-setosa   
3           5.0          3.6           1.4          0.2  Iris-setosa   
4           5.4          3.9           1.7          0.4  Iris-setosa   

   class_idx  
0          0  
1          0  
2          0  
3          0  
4          0  
Count occurence of each class:
class
Iris-versicolor    50
Iris-virginica     50
Iris-setosa        49
Name: count, dtype: int64

Your can learn more about this well established dataset here. In essence, we see measurements of 4 different features and the corresponding type of iris plant out of [‘Iris-setosa’, ‘Iris-versicolor’, ‘Iris-virginica’]. We transform this problem to a logistic regression problem by looking only at two of the classes, which we denote with [0,1]. In addition, we consider only two of the features to make visualization possible.

df = df0[["petal_length", "petal_width", "class_idx"]]
df = df[df["class_idx"] != 0]
df["class_idx"] = df["class_idx"] - 1

print(df["class_idx"].value_counts())
print(df)

class_idx
0    50
1    50
Name: count, dtype: int64
     petal_length  petal_width  class_idx
49            4.7          1.4          0
50            4.5          1.5          0
51            4.9          1.5          0
52            4.0          1.3          0
53            4.6          1.5          0
..            ...          ...        ...
144           5.2          2.3          1
145           5.0          1.9          1
146           5.2          2.0          1
147           5.4          2.3          1
148           5.1          1.8          1

[100 rows x 3 columns]

fig = px.scatter_3d(df[["petal_length", "petal_width", "class_idx"]],
                    x='petal_length',
                    y='petal_width',
                    z='class_idx',
                    color='class_idx',
                    opacity=0.9)

fig.update_layout(margin=dict(l=0, r=0, b=0, t=0))

1.2.3. Preprocess and Dataloader

input_columns = torch.from_numpy(
    df[['petal_length', 'petal_width']].to_numpy()).type(torch.float32)
output_columns = torch.from_numpy(
    df['class_idx'].to_numpy()).type(torch.float32)
output_columns = output_columns.reshape(-1, 1)

print("Input columns: ", input_columns.shape, input_columns.dtype)
print("Output columns: ", output_columns.shape, output_columns.dtype)

Input columns:  torch.Size([100, 2]) torch.float32
Output columns:  torch.Size([100, 1]) torch.float32

# set hyperparameters
batch_size = 25

# create a PyTorch data object used by DataLoader
data = TensorDataset(input_columns, output_columns)

# define data loader which shuffles the data
train_loader = DataLoader(data, batch_size, shuffle=True)

# one batch of training data would look like this:
for x in train_loader:
    print(x, x[0].shape, x[0].dtype)
    break

[tensor([[4.9000, 1.8000],
        [4.9000, 1.5000],
        [4.0000, 1.3000],
        [6.9000, 2.3000],
        [4.2000, 1.3000],
        [4.6000, 1.5000],
        [5.7000, 2.3000],
        [3.6000, 1.3000],
        [3.9000, 1.4000],
        [3.0000, 1.1000],
        [5.7000, 2.5000],
        [6.0000, 2.5000],
        [5.1000, 2.3000],
        [4.8000, 1.8000],
        [4.7000, 1.2000],
        [4.8000, 1.8000],
        [4.1000, 1.0000],
        [5.5000, 1.8000],
        [6.3000, 1.8000],
        [5.2000, 2.3000],
        [4.3000, 1.3000],
        [5.1000, 1.8000],
        [4.8000, 1.8000],
        [4.7000, 1.5000],
        [5.1000, 1.5000]]), tensor([[1.],
        [0.],
        [0.],
        [1.],
        [0.],
        [0.],
        [1.],
        [0.],
        [0.],
        [0.],
        [1.],
        [1.],
        [1.],
        [0.],
        [0.],
        [1.],
        [0.],
        [1.],
        [1.],
        [1.],
        [0.],
        [1.],
        [1.],
        [0.],
        [1.]])] torch.Size([25, 2]) torch.float32

1.2.4. Model and Training

# This is the core part of the logistic regression. Here we define the linear
# transformation of x and afterwards pushing it through sigmoid

# Define model
class LogisticRegression(nn.Module):
    def __init__(self, input_size, output_size):
        super(LogisticRegression, self).__init__()
        self.linear1 = nn.Linear(input_size, output_size)

    def forward(self, x):
        outputs = torch.sigmoid(self.linear1(x))
        return outputs

The torch.nn.BCELoss(h(x),y) function implements \(-\log p(y|x;\vartheta) = - \log \left(h^y(x)(1-h(x))^{1-y}\right)\). Maximizing the probability is the same as minimizing this loss.

# set hyperparameters
learning_rate = 1.0
epochs = 500

input_dim = 2
output_dim = 1

# instantiating the model
model = LogisticRegression(input_dim, output_dim)
criterion = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)

for epoch in range(epochs):
    for x, y in train_loader:

        optimizer.zero_grad()
        outputs = model(x)
        loss = criterion(outputs, y)
        loss.backward()
        optimizer.step()

    print("Epoch: {}. Loss: {}.".format(epoch + 1, loss.item()))

Epoch: 1. Loss: 3.7627408504486084.
Epoch: 2. Loss: 3.8542280197143555.
Epoch: 3. Loss: 2.6949706077575684.
Epoch: 4. Loss: 8.1231050491333.
Epoch: 5. Loss: 3.583245038986206.
Epoch: 6. Loss: 3.732949733734131.
Epoch: 7. Loss: 4.069502353668213.
Epoch: 8. Loss: 0.6965585947036743.
Epoch: 9. Loss: 1.9594788551330566.
Epoch: 10. Loss: 1.0510541200637817.
Epoch: 11. Loss: 2.980556011199951.
Epoch: 12. Loss: 3.93424916267395.
Epoch: 13. Loss: 2.8647773265838623.
Epoch: 14. Loss: 1.8929553031921387.
Epoch: 15. Loss: 5.847078323364258.
Epoch: 16. Loss: 0.5377179980278015.
Epoch: 17. Loss: 8.671006202697754.
Epoch: 18. Loss: 4.262671947479248.
Epoch: 19. Loss: 5.475005626678467.
Epoch: 20. Loss: 0.3305045962333679.
Epoch: 21. Loss: 3.906980514526367.
Epoch: 22. Loss: 3.858604669570923.
Epoch: 23. Loss: 6.744014263153076.
Epoch: 24. Loss: 0.9078060984611511.
Epoch: 25. Loss: 1.9459271430969238.
Epoch: 26. Loss: 1.0113184452056885.
Epoch: 27. Loss: 0.5891411900520325.
Epoch: 28. Loss: 1.1742936372756958.
Epoch: 29. Loss: 0.5662131309509277.
Epoch: 30. Loss: 0.2855275869369507.
Epoch: 31. Loss: 4.35783576965332.
Epoch: 32. Loss: 1.975974440574646.
Epoch: 33. Loss: 0.4330093264579773.
Epoch: 34. Loss: 0.48858270049095154.
Epoch: 35. Loss: 2.090350389480591.
Epoch: 36. Loss: 2.4277312755584717.
Epoch: 37. Loss: 3.3770389556884766.
Epoch: 38. Loss: 2.906691789627075.
Epoch: 39. Loss: 0.3580903708934784.
Epoch: 40. Loss: 1.3845940828323364.
Epoch: 41. Loss: 3.1034364700317383.
Epoch: 42. Loss: 0.6180238127708435.
Epoch: 43. Loss: 1.5651309490203857.
Epoch: 44. Loss: 0.5433673858642578.
Epoch: 45. Loss: 1.104077935218811.
Epoch: 46. Loss: 0.2584732174873352.
Epoch: 47. Loss: 0.33497676253318787.
Epoch: 48. Loss: 0.936159074306488.
Epoch: 49. Loss: 4.383077621459961.
Epoch: 50. Loss: 2.0555739402770996.
Epoch: 51. Loss: 0.20954157412052155.
Epoch: 52. Loss: 0.9594236016273499.
Epoch: 53. Loss: 0.4241853952407837.
Epoch: 54. Loss: 0.5633811950683594.
Epoch: 55. Loss: 0.5446844696998596.
Epoch: 56. Loss: 0.8122733235359192.
Epoch: 57. Loss: 2.5835628509521484.
Epoch: 58. Loss: 1.0829051733016968.
Epoch: 59. Loss: 2.5356318950653076.
Epoch: 60. Loss: 1.2720370292663574.
Epoch: 61. Loss: 0.48374325037002563.
Epoch: 62. Loss: 0.535912811756134.
Epoch: 63. Loss: 0.7364561557769775.
Epoch: 64. Loss: 1.2396310567855835.
Epoch: 65. Loss: 0.30337849259376526.
Epoch: 66. Loss: 0.5147194862365723.
Epoch: 67. Loss: 0.816652774810791.
Epoch: 68. Loss: 0.26882392168045044.
Epoch: 69. Loss: 0.23775644600391388.
Epoch: 70. Loss: 0.13107718527317047.
Epoch: 71. Loss: 0.3698573708534241.
Epoch: 72. Loss: 0.6808709502220154.
Epoch: 73. Loss: 0.44349944591522217.
Epoch: 74. Loss: 0.14446552097797394.
Epoch: 75. Loss: 0.23070082068443298.
Epoch: 76. Loss: 0.6504319906234741.
Epoch: 77. Loss: 0.4169935882091522.
Epoch: 78. Loss: 0.18134312331676483.
Epoch: 79. Loss: 0.22258883714675903.
Epoch: 80. Loss: 0.36729973554611206.
Epoch: 81. Loss: 0.8107978701591492.
Epoch: 82. Loss: 0.4569200575351715.
Epoch: 83. Loss: 0.18886442482471466.
Epoch: 84. Loss: 3.290224313735962.
Epoch: 85. Loss: 0.5581620335578918.
Epoch: 86. Loss: 0.3700585961341858.
Epoch: 87. Loss: 0.35219818353652954.
Epoch: 88. Loss: 1.6059226989746094.
Epoch: 89. Loss: 0.20242159068584442.
Epoch: 90. Loss: 2.0528299808502197.
Epoch: 91. Loss: 2.365645408630371.
Epoch: 92. Loss: 1.3711177110671997.
Epoch: 93. Loss: 0.5599638819694519.
Epoch: 94. Loss: 0.29392796754837036.
Epoch: 95. Loss: 0.1225147545337677.
Epoch: 96. Loss: 0.40621936321258545.
Epoch: 97. Loss: 0.91819167137146.
Epoch: 98. Loss: 2.138803482055664.
Epoch: 99. Loss: 0.33416691422462463.
Epoch: 100. Loss: 0.20578211545944214.
Epoch: 101. Loss: 0.5153934955596924.
Epoch: 102. Loss: 0.10741550475358963.
Epoch: 103. Loss: 0.4751027822494507.
Epoch: 104. Loss: 1.366522192955017.
Epoch: 105. Loss: 0.24443262815475464.
Epoch: 106. Loss: 0.3798985779285431.
Epoch: 107. Loss: 0.2876528203487396.
Epoch: 108. Loss: 0.49070680141448975.
Epoch: 109. Loss: 1.2545077800750732.
Epoch: 110. Loss: 0.8078477382659912.
Epoch: 111. Loss: 0.09937632828950882.
Epoch: 112. Loss: 0.20113199949264526.
Epoch: 113. Loss: 0.15349774062633514.
Epoch: 114. Loss: 0.3075786530971527.
Epoch: 115. Loss: 0.2155229151248932.
Epoch: 116. Loss: 0.10302942246198654.
Epoch: 117. Loss: 0.10130677372217178.
Epoch: 118. Loss: 0.19886308908462524.
Epoch: 119. Loss: 0.3436202108860016.
Epoch: 120. Loss: 0.5447229146957397.
Epoch: 121. Loss: 0.2153213918209076.
Epoch: 122. Loss: 0.10381202399730682.
Epoch: 123. Loss: 0.07022023946046829.
Epoch: 124. Loss: 0.20255175232887268.
Epoch: 125. Loss: 0.07909589260816574.
Epoch: 126. Loss: 0.15371572971343994.
Epoch: 127. Loss: 0.1899891495704651.
Epoch: 128. Loss: 0.18763625621795654.
Epoch: 129. Loss: 0.13862361013889313.
Epoch: 130. Loss: 0.13948161900043488.
Epoch: 131. Loss: 0.11427964270114899.
Epoch: 132. Loss: 0.19699864089488983.
Epoch: 133. Loss: 0.14846853911876678.
Epoch: 134. Loss: 0.3894476294517517.
Epoch: 135. Loss: 1.8745546340942383.
Epoch: 136. Loss: 0.4521435797214508.
Epoch: 137. Loss: 0.2770370841026306.
Epoch: 138. Loss: 0.1706695407629013.
Epoch: 139. Loss: 0.6430865526199341.
Epoch: 140. Loss: 0.8520200252532959.
Epoch: 141. Loss: 0.6013851761817932.
Epoch: 142. Loss: 0.4260537326335907.
Epoch: 143. Loss: 0.07912250608205795.
Epoch: 144. Loss: 0.33515235781669617.
Epoch: 145. Loss: 0.16839376091957092.
Epoch: 146. Loss: 0.1270175576210022.
Epoch: 147. Loss: 0.24437066912651062.
Epoch: 148. Loss: 0.25899991393089294.
Epoch: 149. Loss: 0.28545287251472473.
Epoch: 150. Loss: 0.1813001185655594.
Epoch: 151. Loss: 0.14972692728042603.
Epoch: 152. Loss: 0.11868344992399216.
Epoch: 153. Loss: 0.2360442578792572.
Epoch: 154. Loss: 0.1330283135175705.
Epoch: 155. Loss: 0.3972914218902588.
Epoch: 156. Loss: 1.0658422708511353.
Epoch: 157. Loss: 0.3446771204471588.
Epoch: 158. Loss: 0.9993520379066467.
Epoch: 159. Loss: 0.8740237355232239.
Epoch: 160. Loss: 1.246942400932312.
Epoch: 161. Loss: 0.6797727346420288.
Epoch: 162. Loss: 0.12691743671894073.
Epoch: 163. Loss: 0.22770771384239197.
Epoch: 164. Loss: 0.1999567449092865.
Epoch: 165. Loss: 0.18970000743865967.
Epoch: 166. Loss: 0.5040897130966187.
Epoch: 167. Loss: 0.14001622796058655.
Epoch: 168. Loss: 0.10466977953910828.
Epoch: 169. Loss: 0.22854875028133392.
Epoch: 170. Loss: 0.27898654341697693.
Epoch: 171. Loss: 0.13964423537254333.
Epoch: 172. Loss: 0.7412422299385071.
Epoch: 173. Loss: 0.3123554289340973.
Epoch: 174. Loss: 0.44417160749435425.
Epoch: 175. Loss: 0.5504786968231201.
Epoch: 176. Loss: 0.31456872820854187.
Epoch: 177. Loss: 0.3607586622238159.
Epoch: 178. Loss: 0.7394295334815979.
Epoch: 179. Loss: 0.30807265639305115.
Epoch: 180. Loss: 0.19747154414653778.
Epoch: 181. Loss: 0.20718227326869965.
Epoch: 182. Loss: 0.14167656004428864.
Epoch: 183. Loss: 0.238653302192688.
Epoch: 184. Loss: 0.17307238280773163.
Epoch: 185. Loss: 0.22098495066165924.
Epoch: 186. Loss: 0.23051434755325317.
Epoch: 187. Loss: 0.26954948902130127.
Epoch: 188. Loss: 0.10288310796022415.
Epoch: 189. Loss: 0.04908125847578049.
Epoch: 190. Loss: 0.32968461513519287.
Epoch: 191. Loss: 0.3201558589935303.
Epoch: 192. Loss: 0.27758023142814636.
Epoch: 193. Loss: 0.31535351276397705.
Epoch: 194. Loss: 0.06764908134937286.
Epoch: 195. Loss: 0.0771714523434639.
Epoch: 196. Loss: 0.1657245010137558.
Epoch: 197. Loss: 0.25187721848487854.
Epoch: 198. Loss: 0.09129207581281662.
Epoch: 199. Loss: 0.1280074268579483.
Epoch: 200. Loss: 0.10571141541004181.
Epoch: 201. Loss: 0.1849435567855835.
Epoch: 202. Loss: 0.23951661586761475.
Epoch: 203. Loss: 0.18318510055541992.
Epoch: 204. Loss: 0.06862536817789078.
Epoch: 205. Loss: 0.21230992674827576.
Epoch: 206. Loss: 0.30598247051239014.
Epoch: 207. Loss: 0.05611103028059006.
Epoch: 208. Loss: 0.36917173862457275.
Epoch: 209. Loss: 0.1710907518863678.
Epoch: 210. Loss: 0.3333257734775543.
Epoch: 211. Loss: 0.1613423377275467.
Epoch: 212. Loss: 0.13900351524353027.
Epoch: 213. Loss: 0.3953742980957031.
Epoch: 214. Loss: 0.16565288603305817.
Epoch: 215. Loss: 0.09714675694704056.
Epoch: 216. Loss: 0.1311458945274353.
Epoch: 217. Loss: 0.12129447609186172.
Epoch: 218. Loss: 0.5439049601554871.
Epoch: 219. Loss: 0.2612568140029907.
Epoch: 220. Loss: 0.585618257522583.
Epoch: 221. Loss: 0.6579433679580688.
Epoch: 222. Loss: 0.6218432784080505.
Epoch: 223. Loss: 0.15292789041996002.
Epoch: 224. Loss: 0.4573242962360382.
Epoch: 225. Loss: 0.22231972217559814.
Epoch: 226. Loss: 0.20747822523117065.
Epoch: 227. Loss: 0.22554896771907806.
Epoch: 228. Loss: 0.21338848769664764.
Epoch: 229. Loss: 0.9397063255310059.
Epoch: 230. Loss: 0.2645930349826813.
Epoch: 231. Loss: 0.07754285633563995.
Epoch: 232. Loss: 0.04754773527383804.
Epoch: 233. Loss: 0.26372069120407104.
Epoch: 234. Loss: 0.15019933879375458.
Epoch: 235. Loss: 0.2344370037317276.
Epoch: 236. Loss: 0.2662588357925415.
Epoch: 237. Loss: 0.10683818906545639.
Epoch: 238. Loss: 0.6548510193824768.
Epoch: 239. Loss: 0.3127548396587372.
Epoch: 240. Loss: 0.1952386498451233.
Epoch: 241. Loss: 0.1389436572790146.
Epoch: 242. Loss: 0.2893967628479004.
Epoch: 243. Loss: 0.2714313268661499.
Epoch: 244. Loss: 0.3466980457305908.
Epoch: 245. Loss: 0.2212037593126297.
Epoch: 246. Loss: 0.11697708815336227.
Epoch: 247. Loss: 0.1527465134859085.
Epoch: 248. Loss: 0.2709728479385376.
Epoch: 249. Loss: 0.15831732749938965.
Epoch: 250. Loss: 0.2223861664533615.
Epoch: 251. Loss: 0.2065892219543457.
Epoch: 252. Loss: 0.508756697177887.
Epoch: 253. Loss: 0.21141691505908966.
Epoch: 254. Loss: 0.12251588702201843.
Epoch: 255. Loss: 0.11185552924871445.
Epoch: 256. Loss: 0.2569913864135742.
Epoch: 257. Loss: 0.34633609652519226.
Epoch: 258. Loss: 0.2715227007865906.
Epoch: 259. Loss: 0.17389293015003204.
Epoch: 260. Loss: 0.11943972855806351.
Epoch: 261. Loss: 0.3116445243358612.
Epoch: 262. Loss: 0.25906071066856384.
Epoch: 263. Loss: 0.15291331708431244.
Epoch: 264. Loss: 0.22922033071517944.
Epoch: 265. Loss: 0.06733589619398117.
Epoch: 266. Loss: 0.10854081809520721.
Epoch: 267. Loss: 0.07932312041521072.
Epoch: 268. Loss: 0.19716329872608185.
Epoch: 269. Loss: 0.13675090670585632.
Epoch: 270. Loss: 0.0641201063990593.
Epoch: 271. Loss: 0.13451699912548065.
Epoch: 272. Loss: 0.05020463839173317.
Epoch: 273. Loss: 0.06177259609103203.
Epoch: 274. Loss: 0.07256985455751419.
Epoch: 275. Loss: 0.08938191086053848.
Epoch: 276. Loss: 0.23652498424053192.
Epoch: 277. Loss: 0.14089667797088623.
Epoch: 278. Loss: 0.1492047756910324.
Epoch: 279. Loss: 0.13994695246219635.
Epoch: 280. Loss: 0.1837344765663147.
Epoch: 281. Loss: 0.2665524482727051.
Epoch: 282. Loss: 0.2559693455696106.
Epoch: 283. Loss: 0.24547027051448822.
Epoch: 284. Loss: 0.15372778475284576.
Epoch: 285. Loss: 0.18069715797901154.
Epoch: 286. Loss: 0.1601310670375824.
Epoch: 287. Loss: 0.10171203315258026.
Epoch: 288. Loss: 0.2710087299346924.
Epoch: 289. Loss: 0.10129452496767044.
Epoch: 290. Loss: 0.20965787768363953.
Epoch: 291. Loss: 0.12586309015750885.
Epoch: 292. Loss: 0.4541059136390686.
Epoch: 293. Loss: 0.12281443923711777.
Epoch: 294. Loss: 0.14351096749305725.
Epoch: 295. Loss: 0.24350981414318085.
Epoch: 296. Loss: 0.09975092858076096.
Epoch: 297. Loss: 0.1110764592885971.
Epoch: 298. Loss: 0.19276325404644012.
Epoch: 299. Loss: 0.1307971328496933.
Epoch: 300. Loss: 0.17743118107318878.
Epoch: 301. Loss: 0.11034460365772247.
Epoch: 302. Loss: 0.1748710572719574.
Epoch: 303. Loss: 0.1719467043876648.
Epoch: 304. Loss: 0.12448788434267044.
Epoch: 305. Loss: 0.26585260033607483.
Epoch: 306. Loss: 0.2634234130382538.
Epoch: 307. Loss: 0.12045110017061234.
Epoch: 308. Loss: 0.1697687953710556.
Epoch: 309. Loss: 0.20016229152679443.
Epoch: 310. Loss: 0.14051207900047302.
Epoch: 311. Loss: 0.09726133197546005.
Epoch: 312. Loss: 0.11990151554346085.
Epoch: 313. Loss: 0.10033728927373886.
Epoch: 314. Loss: 0.2470121830701828.
Epoch: 315. Loss: 0.31721559166908264.
Epoch: 316. Loss: 0.3581487238407135.
Epoch: 317. Loss: 0.20331266522407532.
Epoch: 318. Loss: 0.15960761904716492.
Epoch: 319. Loss: 0.16746003925800323.
Epoch: 320. Loss: 0.1318725347518921.
Epoch: 321. Loss: 0.26891592144966125.
Epoch: 322. Loss: 0.0638699159026146.
Epoch: 323. Loss: 0.36458462476730347.
Epoch: 324. Loss: 0.3603992760181427.
Epoch: 325. Loss: 0.7561165690422058.
Epoch: 326. Loss: 0.19434566795825958.
Epoch: 327. Loss: 0.19110558927059174.
Epoch: 328. Loss: 0.32280486822128296.
Epoch: 329. Loss: 0.10958881676197052.
Epoch: 330. Loss: 0.12789537012577057.
Epoch: 331. Loss: 0.14855512976646423.
Epoch: 332. Loss: 0.1312602460384369.
Epoch: 333. Loss: 0.23536470532417297.
Epoch: 334. Loss: 0.10528445988893509.
Epoch: 335. Loss: 0.13980011641979218.
Epoch: 336. Loss: 0.06544208526611328.
Epoch: 337. Loss: 0.18831826746463776.
Epoch: 338. Loss: 0.24939411878585815.
Epoch: 339. Loss: 0.18788856267929077.
Epoch: 340. Loss: 0.1568489372730255.
Epoch: 341. Loss: 0.10017314553260803.
Epoch: 342. Loss: 0.20653373003005981.
Epoch: 343. Loss: 0.1427389681339264.
Epoch: 344. Loss: 0.0916055366396904.
Epoch: 345. Loss: 0.15160708129405975.
Epoch: 346. Loss: 0.1345621794462204.
Epoch: 347. Loss: 0.13858185708522797.
Epoch: 348. Loss: 0.1767992526292801.
Epoch: 349. Loss: 0.14616325497627258.
Epoch: 350. Loss: 0.13161692023277283.
Epoch: 351. Loss: 0.20384138822555542.
Epoch: 352. Loss: 0.4956323206424713.
Epoch: 353. Loss: 0.18888473510742188.
Epoch: 354. Loss: 0.11524703353643417.
Epoch: 355. Loss: 0.0480843223631382.
Epoch: 356. Loss: 0.28324389457702637.
Epoch: 357. Loss: 0.04778691381216049.
Epoch: 358. Loss: 0.17135891318321228.
Epoch: 359. Loss: 0.2510794699192047.
Epoch: 360. Loss: 0.07608583569526672.
Epoch: 361. Loss: 0.10376545041799545.
Epoch: 362. Loss: 0.18284544348716736.
Epoch: 363. Loss: 0.10648760199546814.
Epoch: 364. Loss: 0.0878293588757515.
Epoch: 365. Loss: 0.09376441687345505.
Epoch: 366. Loss: 0.18326988816261292.
Epoch: 367. Loss: 0.11506713181734085.
Epoch: 368. Loss: 0.13349571824073792.
Epoch: 369. Loss: 0.07512111961841583.
Epoch: 370. Loss: 0.28530165553092957.
Epoch: 371. Loss: 0.10291983932256699.
Epoch: 372. Loss: 0.15858674049377441.
Epoch: 373. Loss: 0.10607699304819107.
Epoch: 374. Loss: 0.10975949466228485.
Epoch: 375. Loss: 0.12233569473028183.
Epoch: 376. Loss: 0.2711542546749115.
Epoch: 377. Loss: 0.18217355012893677.
Epoch: 378. Loss: 0.1262475997209549.
Epoch: 379. Loss: 0.06446733325719833.
Epoch: 380. Loss: 0.15895608067512512.
Epoch: 381. Loss: 0.11219919472932816.
Epoch: 382. Loss: 0.2199920415878296.
Epoch: 383. Loss: 0.061199549585580826.
Epoch: 384. Loss: 0.0967867448925972.
Epoch: 385. Loss: 0.27098655700683594.
Epoch: 386. Loss: 0.15658175945281982.
Epoch: 387. Loss: 0.09196043759584427.
Epoch: 388. Loss: 0.10570617020130157.
Epoch: 389. Loss: 0.41173994541168213.
Epoch: 390. Loss: 0.1384175717830658.
Epoch: 391. Loss: 0.06344415992498398.
Epoch: 392. Loss: 0.15987388789653778.
Epoch: 393. Loss: 0.1508321911096573.
Epoch: 394. Loss: 0.32696831226348877.
Epoch: 395. Loss: 0.08989566564559937.
Epoch: 396. Loss: 0.09860123693943024.
Epoch: 397. Loss: 0.05720863863825798.
Epoch: 398. Loss: 0.31362220644950867.
Epoch: 399. Loss: 0.10589691251516342.
Epoch: 400. Loss: 0.22865641117095947.
Epoch: 401. Loss: 0.0690491646528244.
Epoch: 402. Loss: 0.16965904831886292.
Epoch: 403. Loss: 0.060516830533742905.
Epoch: 404. Loss: 0.07338408380746841.
Epoch: 405. Loss: 0.32198596000671387.
Epoch: 406. Loss: 0.08987627178430557.
Epoch: 407. Loss: 0.3607073128223419.
Epoch: 408. Loss: 0.21332193911075592.
Epoch: 409. Loss: 0.06707480549812317.
Epoch: 410. Loss: 0.19396963715553284.
Epoch: 411. Loss: 0.15421198308467865.
Epoch: 412. Loss: 0.18477223813533783.
Epoch: 413. Loss: 0.0915694311261177.
Epoch: 414. Loss: 0.24594822525978088.
Epoch: 415. Loss: 0.10846155136823654.
Epoch: 416. Loss: 0.14441049098968506.
Epoch: 417. Loss: 0.24067804217338562.
Epoch: 418. Loss: 0.20620392262935638.
Epoch: 419. Loss: 0.11360910534858704.
Epoch: 420. Loss: 0.22865581512451172.
Epoch: 421. Loss: 0.45300063490867615.
Epoch: 422. Loss: 0.38209015130996704.
Epoch: 423. Loss: 0.17973437905311584.
Epoch: 424. Loss: 0.1554017812013626.
Epoch: 425. Loss: 0.07620509713888168.
Epoch: 426. Loss: 0.26193228363990784.
Epoch: 427. Loss: 0.15956124663352966.
Epoch: 428. Loss: 0.13435669243335724.
Epoch: 429. Loss: 0.22188644111156464.
Epoch: 430. Loss: 0.09599737077951431.
Epoch: 431. Loss: 0.02657048963010311.
Epoch: 432. Loss: 0.12376344949007034.
Epoch: 433. Loss: 0.19105859100818634.
Epoch: 434. Loss: 0.12635435163974762.
Epoch: 435. Loss: 0.296863317489624.
Epoch: 436. Loss: 0.4021824300289154.
Epoch: 437. Loss: 0.19842411577701569.
Epoch: 438. Loss: 0.22747594118118286.
Epoch: 439. Loss: 0.2806667685508728.
Epoch: 440. Loss: 0.2572818994522095.
Epoch: 441. Loss: 0.24806982278823853.
Epoch: 442. Loss: 0.17973484098911285.
Epoch: 443. Loss: 0.08271142840385437.
Epoch: 444. Loss: 0.07734628766775131.
Epoch: 445. Loss: 0.2300398200750351.
Epoch: 446. Loss: 0.30631065368652344.
Epoch: 447. Loss: 0.0891607403755188.
Epoch: 448. Loss: 0.20881031453609467.
Epoch: 449. Loss: 0.1779317706823349.
Epoch: 450. Loss: 0.2785026431083679.
Epoch: 451. Loss: 0.18024326860904694.
Epoch: 452. Loss: 0.18381038308143616.
Epoch: 453. Loss: 0.23872336745262146.
Epoch: 454. Loss: 0.15693220496177673.
Epoch: 455. Loss: 0.4083346426486969.
Epoch: 456. Loss: 0.14022569358348846.
Epoch: 457. Loss: 0.16338102519512177.
Epoch: 458. Loss: 0.14360027015209198.
Epoch: 459. Loss: 0.26437878608703613.
Epoch: 460. Loss: 0.06526355445384979.
Epoch: 461. Loss: 0.14614368975162506.
Epoch: 462. Loss: 0.14234091341495514.
Epoch: 463. Loss: 0.19047105312347412.
Epoch: 464. Loss: 0.29255998134613037.
Epoch: 465. Loss: 0.14797832071781158.
Epoch: 466. Loss: 0.1974174678325653.
Epoch: 467. Loss: 0.16114825010299683.
Epoch: 468. Loss: 0.16711005568504333.
Epoch: 469. Loss: 0.03187298774719238.
Epoch: 470. Loss: 0.24525290727615356.
Epoch: 471. Loss: 0.24338418245315552.
Epoch: 472. Loss: 0.07824257761240005.
Epoch: 473. Loss: 0.1180843859910965.
Epoch: 474. Loss: 0.17255717515945435.
Epoch: 475. Loss: 0.1716974675655365.
Epoch: 476. Loss: 0.10526850074529648.
Epoch: 477. Loss: 0.21053510904312134.
Epoch: 478. Loss: 0.239199697971344.
Epoch: 479. Loss: 0.05583902820944786.
Epoch: 480. Loss: 0.20926149189472198.
Epoch: 481. Loss: 0.2328605055809021.
Epoch: 482. Loss: 0.06940369307994843.
Epoch: 483. Loss: 0.15140081942081451.
Epoch: 484. Loss: 0.06784144043922424.
Epoch: 485. Loss: 0.05776438117027283.
Epoch: 486. Loss: 0.13888214528560638.
Epoch: 487. Loss: 0.09648612886667252.
Epoch: 488. Loss: 0.10839260369539261.
Epoch: 489. Loss: 0.14974454045295715.
Epoch: 490. Loss: 0.060485027730464935.
Epoch: 491. Loss: 0.11400376260280609.
Epoch: 492. Loss: 0.04561455547809601.
Epoch: 493. Loss: 0.24055945873260498.
Epoch: 494. Loss: 0.03702301159501076.
Epoch: 495. Loss: 0.19121696054935455.
Epoch: 496. Loss: 0.1060003936290741.
Epoch: 497. Loss: 0.22275644540786743.
Epoch: 498. Loss: 0.07407441735267639.
Epoch: 499. Loss: 0.17416444420814514.
Epoch: 500. Loss: 0.3355337381362915.

for name, param in model.named_parameters():
  print(name, ": ", param.data)
# theta_0 = bias, theta_1:2 = weight

# Interpretation:
# linear1.weight :  tensor([[3.4394, 8.9426]])
# -> both parameters are positively correlated, i.e. if any of them increase,
# the probability of having class "1" increases
# linear1.bias :  tensor([-31.8393])
# -> offset prediction by -31.8, which conteracts the large positive weights

linear1.weight :  tensor([[2.9980, 8.9529]])
linear1.bias :  tensor([-26.7381])

x = np.linspace(input_columns[:,0].min(), input_columns[:,0].max(), 10)
y = np.linspace(input_columns[:,1].min(), input_columns[:,1].max(), 10)
xx, yy = np.meshgrid(x,y)
X, Y = xx.flatten(), yy.flatten()
XY = np.vstack([X,Y]).T

with torch.no_grad():
    predicted = model(torch.from_numpy(XY).type(torch.float32)).data.numpy()

predicted = predicted.squeeze()
predicted = predicted.reshape(10,10)

fig = go.Figure(data=[
    go.Surface(
        contours={
            "z": {"show": True, "start": 0.5, "end": 0.5001, "size": 0.05}
        },
        x=x,
        y=y,
        z=predicted,
        opacity=0.5
    ),
    go.Scatter3d(
        x=df["petal_length"],
        y=df['petal_width'],
        z=df['class_idx'],
        mode='markers',
        marker=dict(
            color=df['class_idx'],
            opacity=0.99,
        )
    )
])

fig.update_layout(margin=dict(l=0, r=0, b=0, t=0),
                  scene={
                      "camera_eye": {"x": 7, "y": -3., "z": 0.5},
                      "aspectratio": {"x": 8, "y": 3, "z": 2}
}
)
fig.show()

1.2.5. Exercise

Apply logistic regression to the MNIST handwritten digits dataset. Main differences to the Iris dataset:

• the inputs are images of shape [28,28,1] and need to be flattened out

• the output here is not the probability of being in one class (as in the problem we discusses here), but 10 classes and the probability of being in each of them.

Hint: You might find help here.

####################
# TODO


####################